$ガウスの定理とは任意のベクトル場{\bf A}について$
$以下の式が成り立つことである。$
$$\int_S {\bf A}\cdot {\bf n} dS=\int_V (\nabla \cdot {\bf A}) dV \tag{1}$$
$左辺は{\bf A}の閉曲面S上の面積分を$
$右辺は{\bf A} について$
$ Sで囲まれた領域Vでの体積積分を表す。$
${\bf n}は閉曲面Sの単位法線ベクトルであり $
$領域Vの外を向くように取る。 $
$\nabla (ナブラ)は以下で定義される。$
$$\nabla \equiv \left(\frac{\partial }{\partial x}, \frac{\partial }{\partial y}, \frac{\partial }{\partial z} \right) \tag{2}$$
いかにこの証明を見ていく。
微小直方体について
$それぞれの辺の長さがそれぞれ\Delta x, \Delta y, \Delta z $
$である以下のような微小な直方体を考える。$
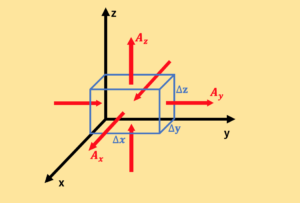
$この時{\bf A}というベクトル場(流体)が$
$直方体の面積を通過する量は$
$その面積分で表されるが、\Delta x, \Delta y, \Delta z が$
$微小であることを考慮すると次のように書ける。$
\begin{eqnarray} &{\bf A}& \cdot {\bf n} dS \\ &=& \{A_x(x+\Delta x, y, z)-A_x(x, y, z) \} \Delta y \Delta z \\ &+& \{A_y(x, y+\Delta y, z)-A_y(x, y, z) \} \Delta z \Delta x \\ &+& \{ A_z(x, y, z+\Delta z)-A_z(x, y, z) \} \Delta x \Delta y \end{eqnarray}
$また、この時\Delta x, \Delta y, \Delta z が微小である事から$
$$ A_x(x+\Delta x, y, z)-A_x(x, y, z)=\frac{\partial A_x}{\partial x}\Delta x $$
$$ A_y(x, y+\Delta y, z)-A_y(x, y, z)=\frac{\partial A_y}{\partial y}\Delta y$$
$$ A_z(x, y, z+\Delta z)-A_z(x, y, z)=\frac{\partial A_z}{\partial z}\Delta z $$
$と表され、$
$この時考えているのは微小直方体のであり$
$\Delta x \Delta y \Delta z=dV とできることから$
\begin{eqnarray} &{\bf A}&\cdot d{\bf S} \\ &=& \left( \frac{\partial A_x}{\partial x}+ \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z} \right) \Delta x \Delta y \Delta z \\&=& \left( \frac{\partial A_x}{\partial x}+ \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z} \right) dV \\ &=& \left (\nabla \cdot {\bf A}\right) dV \tag{3} \end{eqnarray}
$故に{\Large微小直方体については}$
$ガウスの定理(1)が成り立つ事が示された。$
有限の大きさの領域を考える場合
$次に微小ではない有限の大きさをもつ領域$
$について考える。$
$この時は領域を\textcolor{red}{多数の微小直方体から成っている}$
$と考えれば良い。$
$つまり下図のように領域内を区切り$
$微小領域の集合と見る。$
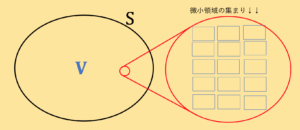
$そして区切ったこのそれぞれの領域について$
$微小領域でのガウスの定理を適応し$
$それらを$
$\textcolor{red}{{\Large積分により足し合わせれば}}良い。$
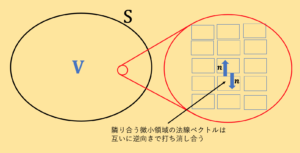
$ S内部の隣り合う領域では$
$お互いに境界面の単位法線ベクトル{\bf n}が$
$\textcolor{red}{逆向きになっており}$
$また、その境界面での流れの大きさは$
$等しいはずなので境界面ではでは\textcolor{red}{打ち消し合う}。$
$そのようにして結局領域Vの$
$\textcolor{red}{内部に含まれる面は寄与せず}$
$その影響が打ち消されない$
$\textcolor{red}{Vの表面について考えている場合と同じ}になる。$
$従ってガウスの定理(1)が成り立つ。$
$$\int_S {\bf A}\cdot {\bf n}dS=\int_V (\nabla \cdot {\bf A}) dV $$
$これは電磁気学で頻繁に用いられる。$
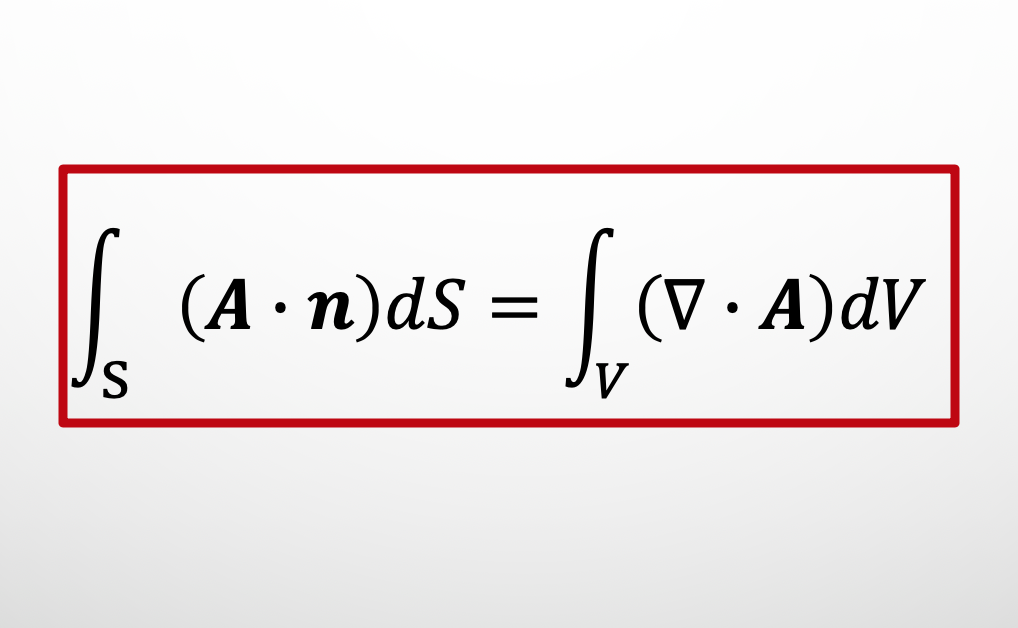
コメントを残す