目次
ガリレイ変換を超えて
ニュートン力学では異なる慣性系の物理はガリレイ変換で結びついている。
しかし、相対論では「光には誰も追いつけない」という事実、つまり
光速度不変の原理
によって明らかにガリレイ変換では不十分なことがわかる。
相対論では、ガリレイ変換の代わりに
ローレンツ変換
を用いることで、異なる慣性系は結びつくことになる。
ローレンツ変換の条件
ではローレンツ変換がどのような変換であるべきかを以下で考えていく。
特殊相対論では光速度不変の原理から
異なる慣性基準形で
世界間隔$s$は不変
ということが導びかれるのだった。
つまり、ローレンツ変換には
世界間隔$s$を
不変する変換
であることが要請される。
では次から具体的にその形を求めていく。
ローレンツ変換の導出
今、異なる2つの慣性基準形$K$と$K’$を考え、両者を結ぶようなローレンツ変換を考える。
両者の間で世界間隔は不変であるので
$$\large s=s’$$
すなわち
$$\small c^2t^2-x^2-y^2-z^2=c^2t’^2-x’^2-y’^2-z’^2\tag{1}$$
これら世界間隔は4次元での”距離”とみなせる。
この世界間隔を不変にする変換として
4次元座標での平行移動と座標の回転が考えられる。
しかし平行移動は空間の原点、または時間の原点をずらすだけでできるので考えるまでもない。
なので考えるべき命題は
世界間隔を不変とするような
座標の回転はどのように表されるか
となる。
4次元での回転は$xy,yz,zx,tx,ty,tz$の6つの平面上での回転の組み合わせで行うことができる。
空間の回転($xy,yz,zx$平面上の回転)について
これは通常の空間の回転として記述でき、
$xy$平面上の回転では、その回転角を$\phi$とすると
$$x=x’\cos\phi-y’\sin\phi\tag{2-a}$$
$$y=x’\sin\phi+y’\cos\phi\tag{2-b}$$
という通常の回転の変換によって世界間隔が不変であり、(1)式が満たされることがわかる。
(他の平面での回転についても同様)
では$tx,ty,tz$平面での回転についてはどうだろうか。
$tx$平面の回転について考えると、この時
$$\large (ct)^2-x^2=(ct’)^2-x’^2\tag{3}$$
が成り立っている必要がある。
これを満たすような回転は、この回転角を$\psi$として(天下り的ではあるが)
$$\ x=x’\cosh\psi +(ct’)\sinh\psi\tag{4-a}$$
$$ct=x’\sinh\psi +(ct’)\cosh\psi \tag{4-b}$$
で与えられる。
これが実際に(3)式を満たすことは、双曲線関数の公式
$$\large \cosh^2\psi-\sinh^2\psi=1 \tag{5}$$
から容易に確かめられる。
その他の平面についても同様に双曲線関数を使って表すことができる。
では具体的に$K$系に対して$K’$が$x$軸方向に速度$V$で運動している場合を考える。
この時2つの座標間で変換されるのは明らかに$x$と$t$であり、また$\psi$は速度$V$に依存することが推測される。
そこでまず$\psi$の$V$依存性を明らかにするため、$K’$の原点の運動を考える。
そこで(4)式に$x’=0$を代入して
$$x=(ct’)\sinh\psi,~~ ct=(ct’)\cosh\psi \tag{6}$$
(ここで$x$は$K$における$K’$の原点の座標であることに注意)
(6)式で得られた2式を用いて
$$\large \frac{x}{ct}=\frac{ct’\sinh\psi}{ct’\cosh\psi}=\tanh\psi$$
上式において$\large \frac{x}{t}=V$であるので、最終的に
$$\large \frac{V}{c}=\tanh\psi\tag{7}$$
が得られ、$V$と$\psi$の関係が明らかになった。
(7)式から双曲線関数の次の公式
$$\cosh^2\psi=\frac{1}{1-\tanh^2\psi}$$
を用いると$\sinh\psi$、$\cosh\psi$の形として
$$\sinh\psi=\frac{\frac{V}{c}}{\sqrt{1-\frac{V^2}{c^2}}}\tag{8-a}$$
$$\cosh\psi=\frac{1}{\sqrt{1-\frac{V^2}{c^2}}} \tag{8-b}$$
がえられる。
これを(4)式に代入して、この場合のローレンツ変換は
$$\large x=\frac{x’+Vt’}{\sqrt{1-\frac{V^2}{c^2}}}\tag{9}$$
$$\large ct=\frac{ct’+\frac{V}{c}x’}{\sqrt{1-\frac{V^2}{c^2}}}\tag{10}$$
$$(y=y’,z=z’)$$
だとわかる。
$K’$が$y,z$方向に運動している場合であっても同様の議論でローレンツ変換を求めることができ、任意の方向に運動している時はその速度を各成分に分け、それぞれの方向のローレンツ変換を組み合わせればいい。
また、(9)(10)式は$K’→K$の変換を表すが、この逆変換($K→K’$)は速度を$V→-V$としたローレンツ変換となる。
ローレンツ変換の行列表示
上で求めた、x方向に速度Vで運動している系との間のローレンツ変換を行列を用いて表すと
$$\left(
\begin{array}{cccc}
\gamma&\beta \gamma &0&0\\
\beta \gamma &\gamma&0&0\\
0&0&1&0\\
0&0&0&1\\
\end{array}
\right)$$
$$\gamma\equiv \frac{1}{\sqrt{1-\frac{V^2}{c^2}}}, \beta \equiv \frac{V}{c}$$
と表され、その変換は
$$\left(\begin{array}{c}ct\\x\\y\\z\\ \end{array}\right)=
\left(
\begin{array}{cccc}
\gamma&\beta \gamma &0&0\\
\beta \gamma &\gamma&0&0\\
0&0&1&0\\
0&0&0&1\\
\end{array}
\right)
\left(
\begin{array}{c}ct’\\x’\\y’\\z’\\ \end{array}\right)
$$
となる。
また上で求めた変換は通常「ローレンツ逆変換」と呼ばれ、
ローレンツ変換は
$$\large x→x’=\Lambda x$$
$$\Lambda=\left(
\begin{array}{cccc}
\gamma&-\beta \gamma &0&0\\
-\beta \gamma &\gamma&0&0\\
0&0&1&0\\
0&0&0&1\\
\end{array}
\right)$$
というような変換をもたらすものとして定義される。
なお、ローレンツ変換(4次元での回転)に加え、冒頭で述べた平行移動による変換まで含めたものを
ポアンカレ変換
と呼ぶ。
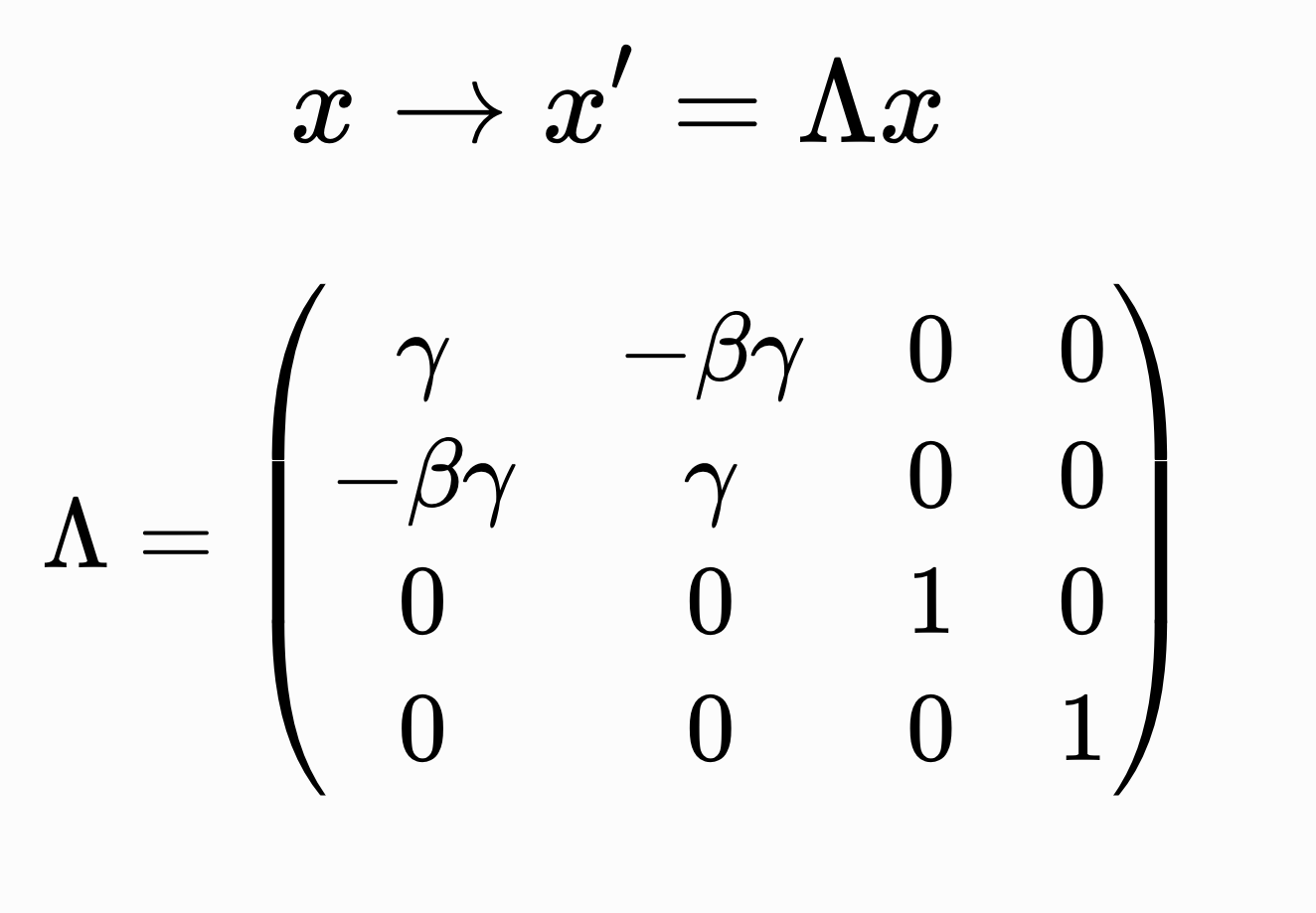
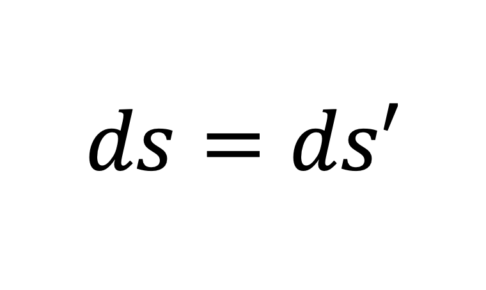

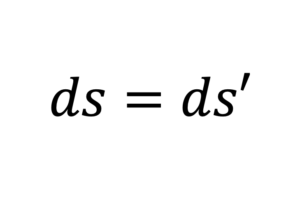

コメントを残す