今回用いるマクスウェル方程式
今回はマクスウェル方程式の4つの式のうち、次の1つを用いる。
$$\nabla \times \boldsymbol{B}-\epsilon_0\mu_0\frac{\partial \boldsymbol{E}}{\partial t}=\mu_0 \boldsymbol{j}\tag{1}$$
$$\big(\mathrm{rot} \boldsymbol{B}-\epsilon_0\mu_0\frac{\partial \boldsymbol{E}}{\partial t}=\mu_0 \boldsymbol{j}\big)$$
ビオ・サバールの法則の導出
有限な運動を行っている電荷の系を考える。
まず先ほどあげたマクスウェル方程式において
その時間平均をとってみる。
すると
$$\nabla \times \overline{\boldsymbol{B}}-\frac{1}{c}\overline{\frac{\partial \boldsymbol{E}}{\partial t}}=\mu_0 \overline{\boldsymbol{j}}\tag{2}$$
が得られる。
ここで(2)式の第2項は0となる。
というのも、$\boldsymbol{E}$が
有限な物理量であるため
その導関数の時間平均は
\begin{align}
\overline{\frac{\partial \boldsymbol{E}}{\partial t}}&=\frac{1}{T}\int^{T}_{0}\frac{\partial \boldsymbol{E}}{\partial t}dt\\
\\
&=\frac{E(T,\boldsymbol{r})-E(0,\boldsymbol{r})}{T}
\end{align}
したがって$T→\infty$となる時
明らかにこの量は0になる。
よって最終的に(2)式は
$$\nabla \times \overline{\boldsymbol{B}}=\mu_0 \overline{\boldsymbol{j}}\tag{3}$$
となる。
このようにして得られた(3)式に
ベクトルポテンシャル$\boldsymbol{A}$を導入すると
$$\nabla \times \overline{\boldsymbol{A}}=\overline{\boldsymbol{B}}\tag{4}$$
と、ベクトルラプラシアンの定義
\begin{align}
\boldsymbol{\bigtriangleup}&=\nabla(\nabla \cdot) – \nabla\times\nabla\times\\
\\
&(=\mathrm{grad}~\mathrm{div}-\mathrm{rot}~\mathrm{rot})
\end{align}
より
$$\nabla (\nabla \cdot \overline{\boldsymbol{A}})-\boldsymbol{\bigtriangleup} \overline{\boldsymbol{A}}=\mu_0 \overline{\boldsymbol{j}}\tag{5}$$
となる。
さらにベクトルポテンシャルの不定性から、この発散が0となるように選ぶようにすると
$$\nabla \cdot \overline{\boldsymbol{A}}=0$$
を代入して
$$\boldsymbol{\bigtriangleup} \overline{\boldsymbol{A}}=-\mu_0 \overline{\boldsymbol{j}}\tag{6}$$
という方程式が得られる。
(6)式はベクトルポテンシャルの各成分ごとにポアソン方程式と同じ形の方程式が成り立つことを意味する。
それゆえこの方程式の解は
ポアソン方程式の解から
$$\overline{\boldsymbol{A}}=\frac{\mu_0}{4\pi}\frac{\overline{\boldsymbol{j}}}{r}$$
となることがわかる。
($r$は電荷の系における電流素片から$\overline{\boldsymbol{A}}$を求めようとする点までの距離)
ここで先程の式は
微小な電流素片のみ
が作るベクトルポテンシャルを
求めているに過ぎないことに
注意が必要。
求めるべきは電荷の系全体が
作るベクトルポテンシャルであるから
ある点におけるベクトルポテンシャルは
それぞれの電流素片が作る
ポテンシャルの重ね合わせ
となる。
よって先程の式を書き直して
最終的にベクトルポテンシャルは
$$\overline{\boldsymbol{A}}=\frac{\mu_0}{4\pi}\int_V \frac{\overline{\boldsymbol{j}}}{r}dV\tag{7}$$
(dVは電荷の系の体積要素を表す)
で与えられる。
(7)式を(4)式に代入して
\begin{align}
\overline{\boldsymbol{B}}&=\nabla \times \overline{\boldsymbol{A}}\\
\\
&=\frac{\mu_0}{4\pi}\int_V \nabla \times \frac{\overline{\boldsymbol{j}}}{r}dV
\end{align}
ここで次のベクトル解析の公式
$$\nabla b\times \boldsymbol{a}=b\nabla \times \boldsymbol{a} + \nabla b \times \boldsymbol{a} $$
($\boldsymbol{a}$はベクトル、$b$はスカラー)
を用いると、微分の際$\overline{\boldsymbol{j}}$は
一定とみなせるので
\begin{align}
\nabla \times \frac{\overline{\boldsymbol{j}}}{r}&=\nabla \frac{1}{r} \times \boldsymbol{j}\\
\\
&=\frac{\overline{\boldsymbol{j}} \times \boldsymbol{r}}{r^3}
\end{align}
が得られる。これを代入して最終的に
$$\overline{\boldsymbol{B}}=\frac{\mu_0}{4\pi}\int_V\frac{\overline{\boldsymbol{j}}\times \boldsymbol{r}}{r^3}\tag{8}dV$$
が得られ、これは
ビオ・サバールの法則である。
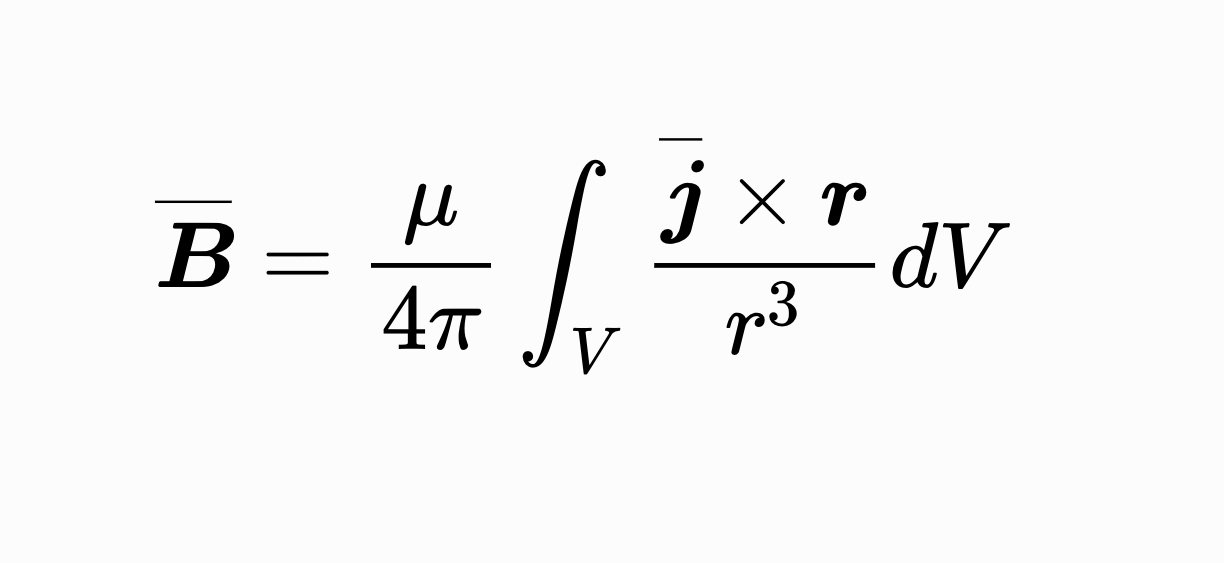
コメントを残す