同次関数におけるオイラーの定理の証明
目次
同次関数におけるオイラーの定理とは
まずn次の同時関数とは
次の条件を満たす関数として定義される。
$$f(ax_1,ax_2\cdots ,ax_m)=a^n f(x_1,x_2\cdots ,x_m)$$
上の条件式を満たす関数を
「n次の同時関数」という。
そしてオイラーの定理とは、n次の同時関数について
\begin{align}
&x_1\frac{\partial f}{\partial x_1}+x_2\frac{\partial f}{\partial x_2}+\cdots+x_m\frac{\partial f}{\partial x_m}\\
\\
&=nf(x_1,x_2\cdots ,x_m)
\end{align}
が成り立つことを言う。
オイラーの定理の証明
簡単のため2変数の場合で証明を行う。
そのために次の式を満たす2変数関数$f(x,y)$を考える。
$$f(ax,ay)=a^nf(x,y)\tag{1}$$
(1)式の右辺について、
$u=ax,v=ay$とおき、$a$で微分すると
\begin{align}
\frac{\partial f}{\partial a}&=\frac{\partial f}{\partial u}\frac{\partial u}{\partial a}+\frac{\partial f}{\partial v}\frac{\partial v}{\partial a}\\
\\
&=\frac{\partial f}{\partial u}x+\frac{\partial f}{\partial v}y \tag{2}
\end{align}
また(1)式の左辺について、
$a$で微分すると
$$na^{n-1}f(x,y)\tag{3}$$
(2)式と(3)式から
$$\frac{\partial f}{\partial u}x+\frac{\partial f}{\partial v}y=na^{n-1}f(x,y)\tag{4}$$
が得られる。
(4)式において、$a→1$とすると
$u→x,v→y$となるので、
$$\frac{\partial f}{\partial x}x+\frac{\partial f}{\partial y}y=nf(x,y)\tag{5}$$
が得られる。
(証明終)
物理における応用
以上のオイラーの定理の物理への応用例として、
ラグランジアン(L)から
エネルギー(E)の表式の導出がある。
(孤立系の)ラグランジアンは
一般座標をqを用いて
$$L=T(q,\dot{q})-U(q)\tag{6}$$
(T:運動エネルギー、U:ポテンシャルエネルギー)
と表され、エネルギーEは
$$E=\Sigma_i \dot{q}_i\frac{\partial L}{\partial \dot{q}_i}-L\tag{7}$$
(ただし和は質点についてとる)
と表される。
ここで運動エネルギーTは$\dot{q}_i$の
2次関数として表されるので
$T$は2次の同次関数である。
よって、同次関数におけるオイラーの定理から
$$\Sigma_i \dot{q}_i\frac{\partial L}{\partial \dot{q}_i}=\Sigma_i \dot{q}_i\frac{\partial T}{\partial \dot{q}_i}=2T\tag{8}$$
が得られる。
(8)式の結果を(7)式に代入して
$$\Large E=T(q,\dot{q})+U(q)$$
というエネルギーの表式がより一般的に得られる。
参考:力学 ランダウ=リフシッツ理論物理学教程
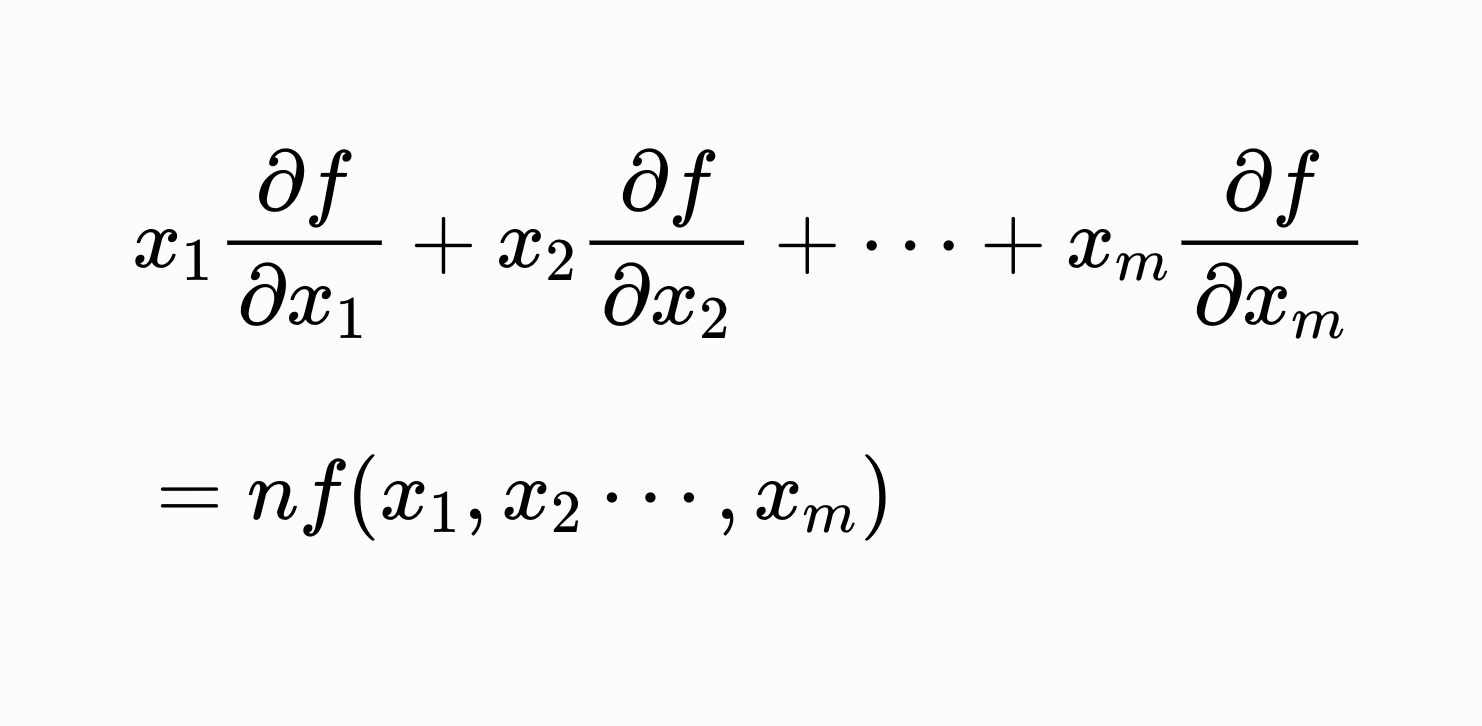
コメントを残す