目次
今回用いる前提事項
今回は次の事項を前提とし、特に議論しない。
- 世界間隔($s$)が異なる座標系で不変であること
なお、上記のことについては以下参照
固有時間
任意の運動をしている時計を考える。
任意の運動をしていてもその瞬間瞬間では一様な運動をしているとみなせ、慣性系としても扱っていいことになる。
この時、観測者の系を$S$系、(各瞬間に)時計に結びついて時計と一緒に運動している座標系を$S’$系とすると、S系で時間が$dt$、S’系で$dt’$だけ経過する間に世界間隔が不変であることから次式が成り立つ。
$$\large ds^2=c^2dt^2-dx^2-dy^2-dz^2=c^2dt’^2\tag{1}$$
これを整理して
\begin{equation}
\begin{split}
\large dt’^2&=\large dt^2-\frac{dx^2+dy^2+dz^2}{c^2}\\
\\
\large dt’&=\large dt\sqrt{1-\frac{dx^2+dy^2+dz^2}{c^2dt^2}}\\
\\
&\frac{dx^2+dy^2+dz^2}{dt^2}=v^2なので(vは速度)\\
\\
\large dt’&=\large dt\sqrt{1-\frac{v^2}{c^2}}
\end{split}
\end{equation}
のように、最終的に
$$\large dt’=\large dt\sqrt{1-\frac{v^2}{c^2}} \tag{2}$$
が得られる。
この両辺を積分することにより
$$\large t’_2-t’_1=\int_{t_1}^{t_2}\sqrt{1-\frac{v^2}{c^2}}dt \tag{3}$$
が得られる。
時計の運動が一様な場合には、$v$が定数となるので(3)式は
$$\large \Delta t’=\sqrt{1-\frac{v^2}{c^2}} \Delta t \tag{4}$$
となる。
ここで$\Delta t’\equiv t’_2-t’_1$、$\Delta t \equiv t_2-t_1$。
(4)式における左辺($\Delta t’$)は時計と一緒に運動している系で流れる時間を表しており、これを「固有時間」と言う。
「時間が遅れる」とは
よく
速い速度で運動するほど
時間が遅れる
のような言い方がされるが、これは先に述べた結果から得られる。
(4)式を再び書くと
$$\large \Delta t’=\sqrt{1-\frac{v^2}{c^2}} \Delta t $$
であるが、この式において
$$\large 0<\sqrt{1-\frac{v^2}{c^2}}<1$$
なので
$$\large \Delta t'<\Delta t$$
が成り立つ。
これは観測者の系で経過する時間よりも時計と一緒に運動している系で経過する時間の方が短いことを意味しており、これが「時間の遅れ」である。
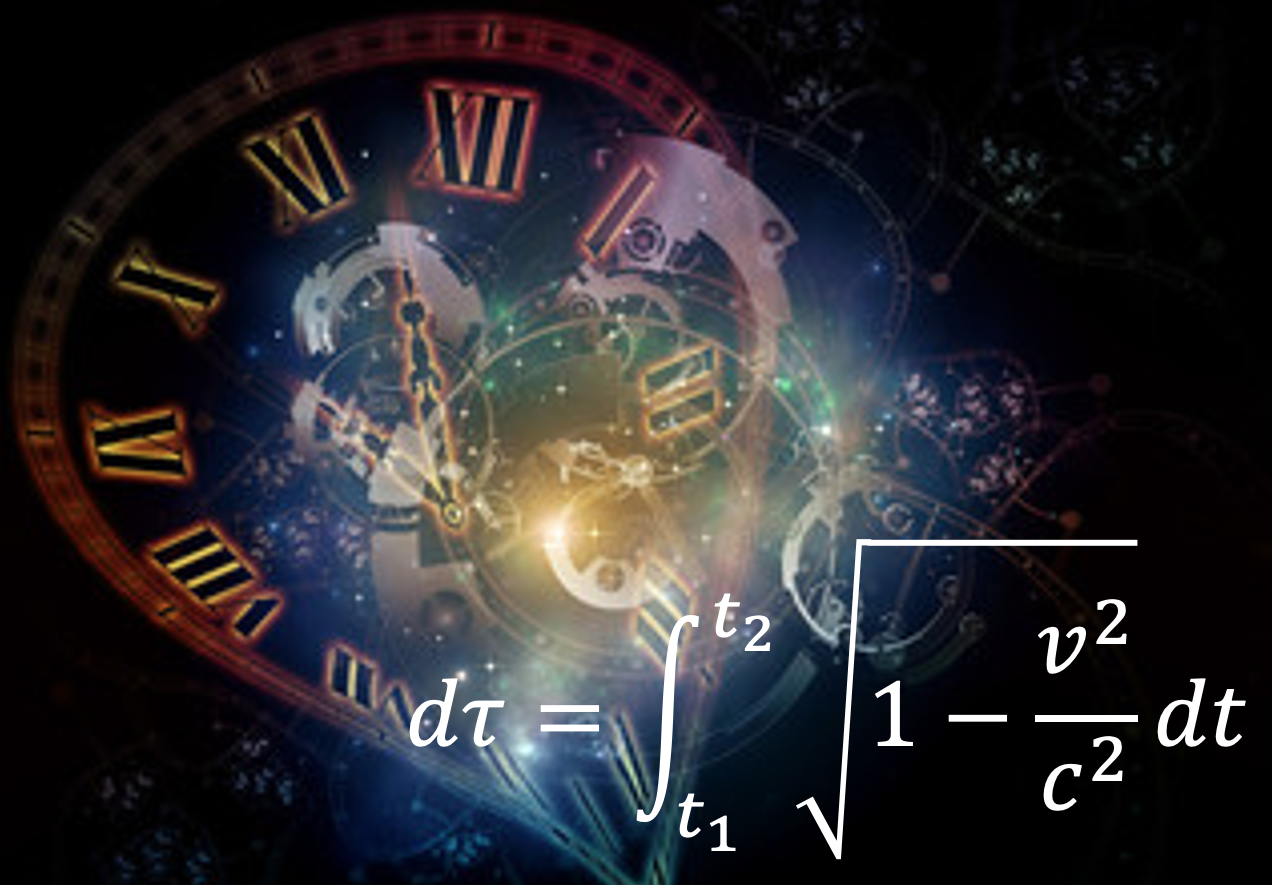
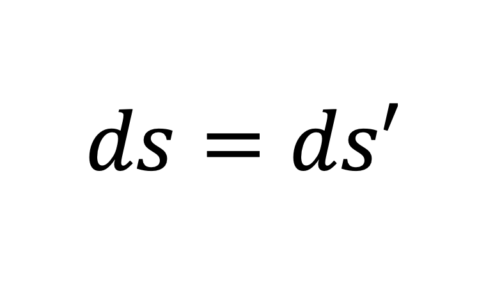
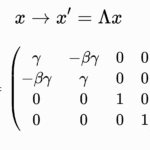
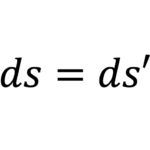
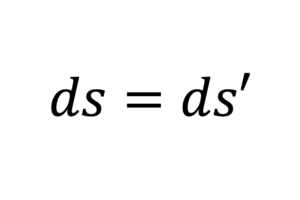
コメントを残す