目次
光速度不変の原理
特殊相対論では
あらゆる慣性系で
光速度は一定である
という原理がその出発点となる。
つまり、たとえジェットコースターに乗っていても、とても速いスポーツカーに乗っていても、新幹線に乗っていても、光に「追いつく」ことは全くできず、どんな状況からしても光は同じ速度を持って走るわけである。
光速度で伝播する信号
ある座標系$S$系において、時刻$t_1$に座標$(x_1,y_1,z_1)$から光速度の信号を送り出し、時刻$t_2$に$(x_2,y_2,z_2)$へそれが到着する場合を考え、それぞれ事象1と事象2とする。
この時信号の伝播した空間的距離は$\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}$であり、また光速度を$c$とおくと、信号はその速さで伝播するので、その距離はまた$c(t_2-t_1)$と書かれる。
故に
$$(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2=c^2(t_2-t_1)^2\tag{1}$$
が成り立つ。
(1)式は左辺を移項して次のようにも書ける。
$$c^2(t_2-t_1)^2-(x_2-x_1)^2-(y_2-y_1)^2-(z_2-z_1)^2=0\tag{2}$$
次にこれらの事象を$S$系に対して相対速度を持つ別の座標系$S’$からみる場合を考える。
$S’$において事象1の座標を$x_1’,y_1’,z_1′,t_1’$で、事象2の座標を$x_2’,y_2’,z_2′,t_2’$で表すと、先ほどと同じように
$$c^2(t_2′-t_1′)^2-(x_2′-x_1′)^2-(y_2′-y_1′)^2-(z_2′-z_1′)^2=0\tag{3}$$
と書ける。上式で光速度が不変であることから $c$は共通であることに注意。
ここで2つの事象間で
$$s_{12}=\{c^2(t_2-t_1)^2-(x_2-x_1)^2-(y_2-y_1)^2-(z_2-z_1)^2\}^{\frac{1}{2}}\tag{4}$$
という量を定義すると、上の結果からある系(今の場合$S$系)で$s_{12}=0$ならば他の系($S’$系)でもそれは0になることがわかる。
この量$s$のことを「世界間隔」といい、これは4次元時空上の仮想的な距離とみなせる。
上の結果はある座標系で世界間隔が0ならば、他の系でも同じく世界間隔が0になることを示す。
時空上で2つの事象が無限に「近い」場合には、世界間隔$ds^2$は
$$\large ds^2=c^2dt^2-dx^2-dy^2-dz^2\tag{5}$$
と書かれる。
相対運動をしている異なる座標系における世界間隔の関係
ある座標系で世界間隔が0ならば、他の座標系でも世界間隔が0になることがわかった。
次に知りたいのは異なる座標系間での、一般的な世界間隔($ds$と$ds’$)を結ぶ関係式である。
- ある座標系で世界間隔が0ならば他の座標系でも世界間隔が0になる
- (世界間隔の定義式から)$ds^2$と$ds’^2$は同じ次数
という2つの条件から$ds^2$と$ds’^2$を結ぶ数式は
$$\large ds^2=\alpha ds’^2 \tag{6}$$
というように、係数$\alpha$を通じて結ばれることが推測される。
では$\alpha$が満たすべき条件を考える。
まず$\alpha$は2つの座標系の「相対速度の絶対値」にのみ依存することができ、$\alpha(V)$と書けると考えられる。
なぜなら$\alpha$が時空上の座標に依存することは、時空上の異なる点ではその対応則(6)式がそれぞれ異なることを意味するが、これは「時間と空間の一様性」から明らかに反する。
また、速度の向きによってその対応則(6)式が変わることは「空間の等方性」に反する。
その結果(6)式は
$$\large ds^2=\alpha(V) ds’^2\tag{7}$$
$$(Vは相対的な速さ)$$
と書ける。
もっと詳しく$\alpha(V)$を求めるために、3つの異なる系$S,S_1,S_2$を考え、$S$系からみた系$S_1,S_2$の(相対)速度を$V_1,V_2$、また($S$系からみた)系$S_2$の系$S_1$に対するの相対速度を$V_{12}$とすると、今
$$ds^2=\alpha(V_1) ds_1^2$$
$$ds^2=\alpha(V_2)ds_2^2$$
$$ds_1^2=\alpha(V_{12})ds_2^2$$
という3つの関係式が得られることになる。
これらの式から
比を考えることによって
$$\large \frac{\alpha(V_2)}{\alpha(V_1)}=\alpha(V_{12})\tag{8}$$
が得られる。
ここで$V_{12}$は$S_1,S_2$の速度$\vec{V_1},\vec{V_2}$の絶対値だけでなく、それらがなす角度に依存するはずである。
しかし(8)式は$V_{12}$が速度$\vec{V_1},\vec{V_2}$の絶対値だけに依存していることを意味する式となっている。
このことから$\alpha$は$V$の関数ではなく定数であることがわかる。
そしてその定数は(8)式を満たすことから、
$$\Large \alpha = 1$$
とわかる。
以上のような議論から、最終的に
$$\Large ds^2=ds’^2 \tag{9}$$
という帰結が得られ
世界間隔は
異なる慣性系で不変
ということが言える。
この(9)式は相対論における光速度不変の原理の数学的定式化とも言える。
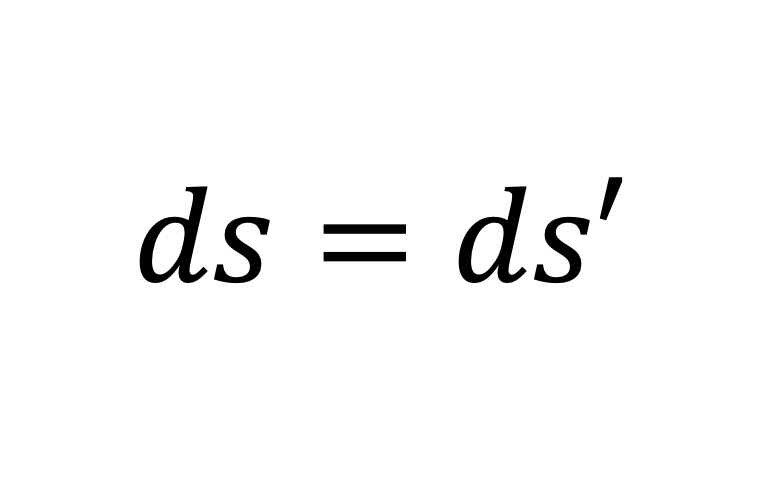


コメントを残す